皆様こんにちは!修士1年の河竹純一です.
前回の巨大数論の解説ではヒドラゲームを紹介し,巨大数を作ることは強い関数を作ることと同義であるとして話を終えました.(前回の記事はコチラ)
今回は”強い”関数とは実際にどういうことなのか,例としてアッカーマン関数を挙げて説明をしようと思います.
アッカーマン関数の説明の前に,普段私たちが日常的に使う関数がどのような性質を持っているかを理解する必要があります.
代表的な増加関数を考えると,足し算や掛け算などの四則演算を使った関数や冪乗を使った指数関数あたりがすぐに思いつくと思います.
これらの関数には以下のような関係性があります.
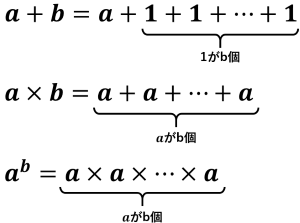
したがって,掛け算は足し算の,冪乗は掛け算のそれぞれ反復であることがわかります.
このことを原始再帰と呼び,原始再帰の性質を持つ関数を原始再帰関数と呼びます.
原始再帰を繰り返すことで以下のように拡張することができます.
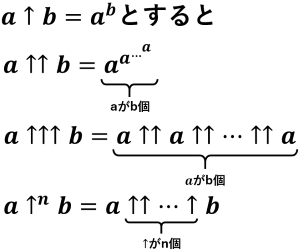
上記の上矢印を使った表記をクヌースの矢印表記と呼びます.(クヌースの矢印表記を発明したドナルド・クヌースはコンピュータの組版TEXの開発者でもあります)
また,これらの原子再帰関数を一般化したものをハイパー演算と呼び,加算,乗算,冪乗をそれぞれハイパー1,ハイパー2,ハイパー3と表すことができます.つまり,加算はハイパー0(後者関数:f(n)=n+1)の原子再帰によって,乗算はハイパー1の原始再帰によって,冪乗はハイパー2の原始再帰によって計算されるのです.
したがって,ハイパー演算子とクヌースの矢印表記の間には次の関係性があることがわかります.

以上の原始再帰関数を踏まえて,以降アッカーマン関数の説明に入ります.
アッカーマン関数
アッカーマン関数は以下で定義される関数であり,原始再帰関数よりも強い関数となっています.

一見しただけではその大きさがよくわからないのでいくつか具体的な数字を代入してみます.
まず,A(1, 1)を計算してみると
A(1, 1)=A(0, A(1, 0)) ←3番目の式
=A(0, A(0, 1)) ←2番目の式
=A(0, 2) ←1番目の式
=3
これは簡単ですね.
次にA(2, 2)を計算してみます.
A(2, 2)=A(1, A(2, 1))
=A(1, A(1, A(2, 0)))
=A(1, A(1, A(1, 1)))
=A(1, A(1, A(0, A(1, 0))))
=A(1, A(1, A(0, A(0, 1))))
=A(1, A(1, A(0, 2)))
=A(1, A(1, 3))
=A(1, A(0, A(1, 2)))
=A(1, A(0, A(0, A(1, 1))))
=A(1, A(0, A(0, 3))) ←A(1, 1)=3
=A(1, A(0, 4))
=A(1, 5)
=A(0, A(1, 4))
=A(0, A(0, A(1, 3)))
=A(0, A(0, 5)) ←A(1, 3)=5
=A(0, 6)
=7
だんだんと階層が増えてきました
しかしながら数そのものは急激に増えそうな気配がありません.
手計算ではそろそろ面倒になってきたので,プログラムを作ってコンピュータに計算してもらうことにします.
Pythonで以下のような関数を作りました.
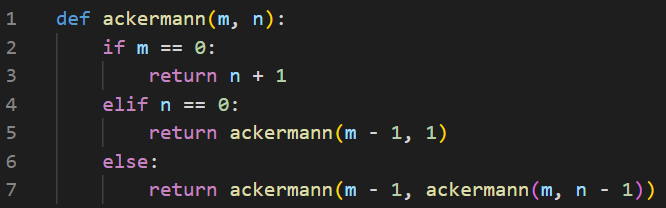
この関数に(0, 0), (0, 1), (0, 2), … , (0, 9), … , (9, 9)を代入してみました.その結果が以下です.
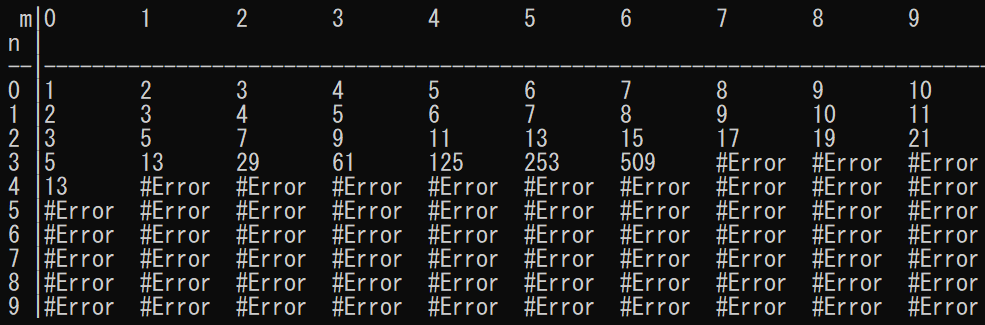
途中からエラーでプログラムが出力されていないことがわかります.
このエラーはRecursionErrorというエラーで再帰の回数の上限を突破したときに起きるエラーです.
この上限はPythonであればデフォルトで1000になっているので1000以上の値が出力されないということです.
実はアッカーマン関数は矢印表記を使って以下のように表すことができます.
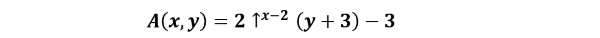
これにしたがってA(4, 1)以降を計算すると以下のようになります.
A(4, 1)=65533
A(4, 2)≈2×10^19728
A(4, 3)≈10(^6×10(^19728))
A(5, 1)=2(↑↑65536)-3
以上のことからアッカーマン関数は第一引数を1増やすと↑が一本増える関数であるということがわかりました.
単純に↑が増えるだけというと大したことがなさそうに見えますが,たった1増やすだけで足し算が掛け算に,掛け算が冪乗になる程度の増加具合であるということです.
この増加速度はどんな原始再帰関数よりも速いため,”強い”関数となっています.
アッカーマン関数のような再帰をする関数を2重再帰関数と呼びます.
1回1回の操作自体は1+1を繰り返しているだけなのですが,2重再帰関数ではとある原子再帰関数に対して再帰する回数を指定することによって数を爆発的に増やしているのです.
ここまででアッカーマン関数の説明をしましたが,巨大数論のほんの一歩目に過ぎません.
次回はふぃっしゅ数バージョン1か順序数あたりについて解説しようと思います.